leetcode经典面试150题

数组/字符串

删除有序数组中的重复项2

题目

给你一个有序数组 nums ，请你原地删除重复出现的元素，使得出现次数超过两次的元素只出现两次 ，返回删除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

并需要返回数组的长度

接口

class Solution {
    public int removeDuplicates(int[] nums) {
    }
}

思路

注意提供给我们的数组就是有序的，说明相同的元素是出现在一起的 为了让解法更具有一般性，我们将原问题的「保留 2 位」修改为「保留 k 位」。 由于是保留 k 个相同数字，对于前 k 个数字，我们可以直接保留 对于后面的任意数字，能够保留的前提是：与当前写入的位置前面的第 k 个元素进行比较，不相同则保留——这就是全题目的重点，如果与其前面的第k个数相同，就说明这一个数字出现超过了k个，新读取的数并不能被保留到数组中

解法

遇到操作数组的题目，而且是要删除/移动数组内容的情况，一般来说会使用双指针法。这里也是一样，先设置一个慢指针slow = k（slow指针之前的内容都是有效的数，已经被录入了最终返回的数组，初始时有0~k-1一共k个元素），然后设置快指针fast = k（fast指针每次循环都会向后移动一位，进行数组遍历）

在进行遍历的过程中进行思路中的操作——与当前写入的位置前面的第 k 个元素进行比较：

如果不一样就保留：保留的操作就是将fast指针遍历到的那个数移动到slow指针的位置（即新遍历到的数加入数组），然后由于有效的数多了一个，slow指针需要向后移动一位，即nums[slow] = nums[fast];slow++; 如果一样就舍去：舍去就是不管当前fast遍历到的元素，直接忽略不做操作 最后都需要将fast指针后移一位继续遍历

双指针的代码如下：

class Solution {
    public int removeDuplicates(int[] nums) {
        int k = 2;
        if(nums.length <= k) return nums.length;
        //初始化双指针
        int slow = k,fast = k;//第k+1个数
        while(fast < nums.length){
            if(nums[fast] != nums[slow-k]){//没有超过k个数
                nums[slow] = nums[fast];
                slow++;
            }
            fast++;
        }
        return slow;
    }
}

在题解中看到宫水三叶大佬的代码是：

class Solution {
    public int removeDuplicates(int[] nums) {
        return process(nums, 2);
    }
    int process(int[] nums, int k) {
        int u = 0;
        for (int x : nums) {//遍历数组
            //如果u < k，代表慢指针（有效的数）比k小，不可能有数被遗弃，所以需要将新遍历到的数纳入有效数组
            //如果nums[u - k] != x，代表快指针遍历到的数并不是他前面第k个数，表示并没有超出限额，所以也将新遍历到的数纳入分组
            //nums[u++] = x，表示将当前遍历到的数x放入到当前慢指针u的位置，并把慢指针u向后移动一位，即将新遍历到的数纳入分组的代码实现
            if (u < k || nums[u - k] != x) nums[u++] = x;
        }
        return u;
    }
}

这个代码更加简洁，但是方法还是一样的，并不要求掌握，只是学习下别人的代码风格

多数元素

题目

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例

输入：nums = [3,2,3]
输出：3

接口

class Solution {
    public int majorityElement(int[] nums) {
  }
}

思路

一开始就想到了可以建立一个映射，将每一个数出现的次数用一个HashMap存储下来，每次遍历的时候顺便看下刚刚添加进数的那个HashMap的value是否超过了n/2，我想这就是最简单、直接的思路了，顺便可以复习一下HashMap的语法： Map.put(key,value) Map.get(key) Map.getOrDefault(key,defaultNum) 我的代码如下：

import java.util.HashMap;
import java.util.Map;


class Solution {
    public int majorityElement(int[] nums) {
        Map<Integer, Integer> countMap = new HashMap<>();
        int majorityThreshold = nums.length / 2;


        for (int num : nums) {
            countMap.put(num, countMap.getOrDefault(num, 0) + 1);
            if (countMap.get(num) > majorityThreshold) {
                return num;
            }
        }
        // 由于题目保证存在多数元素，这里不需要返回其他值
        return -1; // 这行代码实际上不会执行
    }
}

进阶

后面我看到了一行进阶挑战：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

进阶思路

摩尔投票法 图片描述 所以，如果遍历的过程中当前数组段的vote为0的话，就说明这段数组及以前之前还没有分出胜负，所以在未遍历的数组中，vote肯定是要>0的

而且，因为题目说了一定存在多数元素，所以其实每一段到底是谁赢了并不重要，因为只要多数元素赢的比重大就可以了——如果不是多数元素赢的比重大，那么就会发现并不存在>n/2次出现的元素，不如说右上图中如果数组是：

2213/3354/2

那么就不存在多数元素

进阶代码

class Solution {
    public int majorityElement(int[] nums) {
        int x = 0, votes = 0;
        for (int num : nums){
            if (votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        return x;
    }
}

轮转数组

题目

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。默认读取的是nums数组

接口

class Solution {
    public void rotate(int[] nums, int k) {
    }
}

思路

若k比数组长度长，则将k转化为一个周期内的数 没有越界的就向右移动k位 如果越界，那么就用mod操作判定移动到哪里

代码

class Solution {
    public void rotate(int[] nums, int k) {
        k = k % nums.length;
        int[] ret = new int[nums.length];
        for(int i = 0;i < nums.length;i++){
            ret[((i+k)%nums.length)] = nums[i];
        }
        for(int i = 0;i < nums.length;i++){
            nums[i] = ret[i];
        }
    }
}

进阶

你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗

进阶思路

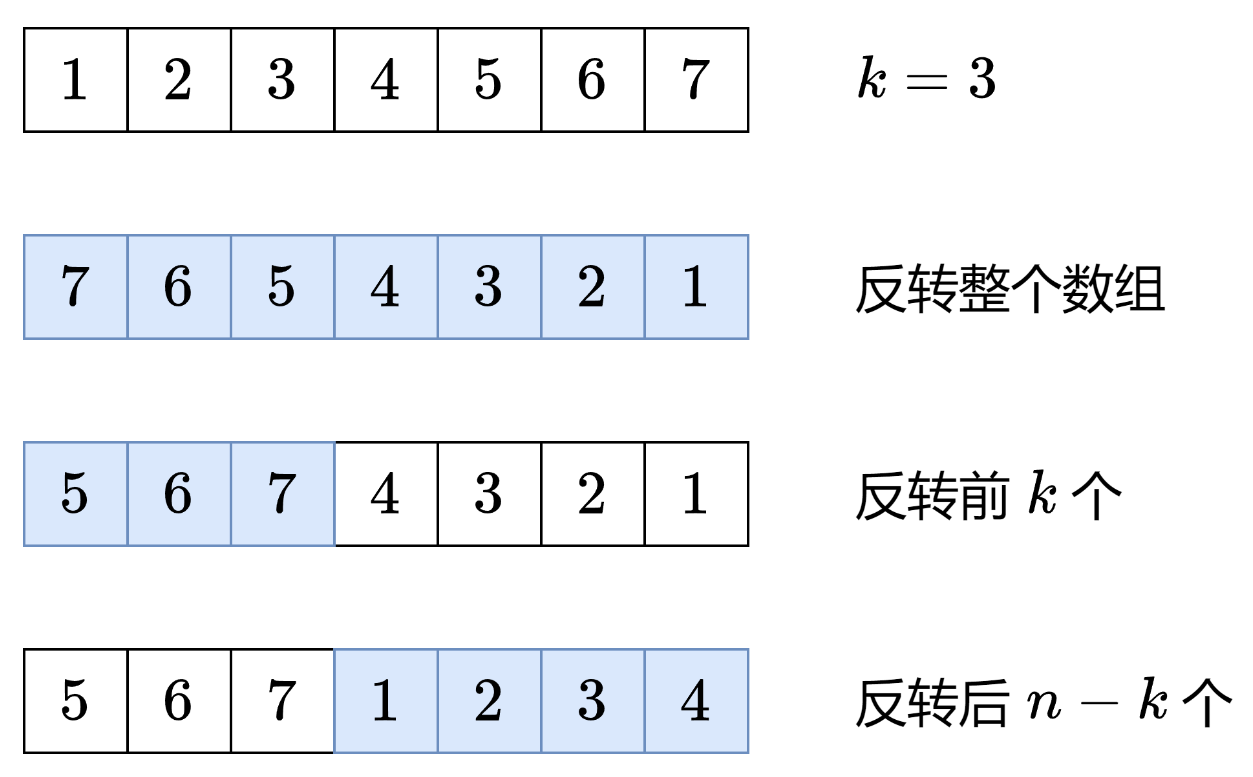
如下图所示，我们可以这样来理解向右移动k位：

后k个元素变成了前k个元素——去反转整个数组 但是前、后两段内部在整个数组反转时候也被反转了——那么重新再反转前k个和后n-k个元素 图片描述

进阶代码

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n; // 轮转 k 次等于轮转 k%n 次
        reverse(nums, 0, n - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, n - 1);
    }


    private void reverse(int[] nums, int i, int j) {
        while (i < j) {
            int temp = nums[i];
            nums[i] = nums[j];
            nums[j] = temp;
            i++;
            j--;
        }
    }
}